Excelのゴールシークを使って「$x^x=2$」を満たす実数$x$（近い数）を求めてみよう

今回は、エクセルの便利機能「ゴールシーク」についてです。

タイトルの数式「$x^x=2$」

一見シンプルな式ですが「これだ！」という$x$を簡単に求めることって意外と難しいですよね。

今回はExcelの「ゴールシーク」という機能を使って『$x^x=2$　となる　$x$』（に近い数）を見つける方法を紹介します。

この式だけでなく、ちょっとした計算や方程式を解くのにも使えるので、この機会に『ゴールシーク』の使い方をマスターしちゃうのも良いかも知れません。

Excelの機能「ゴールシーク」について

Excelの機能「ゴールシーク」を知っていますか？

ゴール（Goal）・シーク（Seek）という名前が表す通り「答えを探してくれる」機能で、上手く使うと面倒な計算をサクッと終わらせることができちゃうんです。


ゴールシークを使うとその条件になる$x$を逆算して求めることができるので、方程式の解を知りたい時にも活用できます。

・$2x+5 = 11$となる$x$が知りたい時
・$2x^2=52$となる$x$が知りたい時

ほかにも、もう少し複雑な計算でも大丈夫。

・$x^3+x^2-5x+10 = 12$となる$x$が知りたい時

などなど。

ゴールシークの使い方を実例で紹介

ゴールシークの使い方を実例を使って紹介します。

例えば、$2x^2=52$という式を考えます。この式を満たす「$x$」を知りたい時、

普通なら方程式を解いていろいろと計算して答え（$\sqrt{26}$）を求めますが、今回はExcelを使って求めてみます。

①Excelシートで式を入力する

・数式：$2x^2=y$
・条件：$y=52$となる$x$を知りたい

まず、Excelのシートに「変化させるセル」と「数式を入力したセル」を用意します。

下の画像では、「変化させるセル（$x$）」としてC3のセルに数値「1」（ゴールシークの初期値）、「数式を入力したセル」としてC4のセルに「=2*C3^2」と入力。

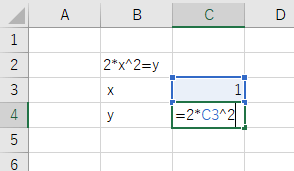
「C3」のセルには$x$の値として仮に1を（1じゃなくても好きな数で良いです）、
「C4」のセルは式の答え$y$として数式「=2*C3^2」を入れます。

②ゴールシークを起動して条件を入力する

次にメニューの中の「データ」を選び、右の方にある「What-If分析」をクリック、開くリストの中から「ゴールシーク」を選択します。

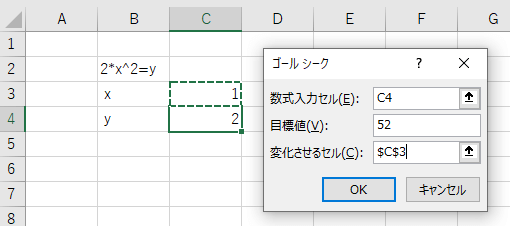
そうすると下の画像のようにゴールシークの条件入力画面が開きます。

「数式入力セル」　：C4を選択
「目標値」　　　　：「52」　　※今回のyの値（計算結果）
「変化させるセル」：C3を選択　※変数$x$

このように設定して「OK」を押すと計算がスタートします（答えが出るまで少し待つ）。

計算はコンピューターが力技で、$x$に数値をどんどん代入して試しているようです。

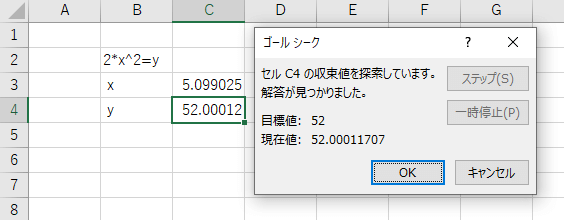
無事に答え（に近い数）が見つかると、下の画像のように解答が見つかりましたと知らせてくれます。

今回の解答（$x$）は5.099025で、その時の値（$y$）は52.00011707となっています。

ただし、計算に時間がかかり過ぎるようだと答えが見つかっていなくても勝手に処理を打ち切られてしまうことがあるので注意してください。

そんな時は、$x$の初期値を変えてみるか、数式を少し変形して入力してやると上手くいくことがあります（指数⇔対数、など）。

本当の解とゴールシークの解答を見比べてみる

今回の結果について念のため確認しておきます。

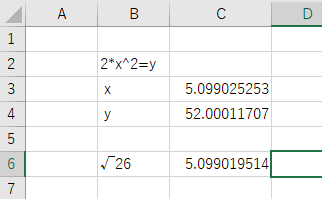
数式「$2x^2=52$」の方程式を解いて求められる$x$の値$\sqrt{26}$は5.099019514です。

一方、今回ゴールシークで出た解答5.099025253となっていて、方程式をちゃんと解いた時とかなり近い値となっています。

今回の例のように、ゴールシークは下のような時に使える機能です。

・計算式が出来ていて（$2x^2=y$）
・式の結果の数値が先に決まっていて（$y=52$）
・その結果になる数$x$を知りたい

つまり、今回のタイトルの式$x^x=2$でも使えるに違いない！！
というわけで、実際にやってみました。

$x^x=2$となる$x$をゴールシークで求めてみる。

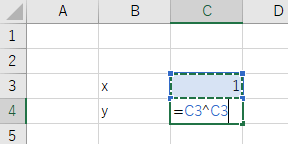
今回は計算式（C4のセル）を「=C3^C3」と入力します。

その他は上の例とほとんど同じです。下の画像のようにあらかじめ入力しておいて。

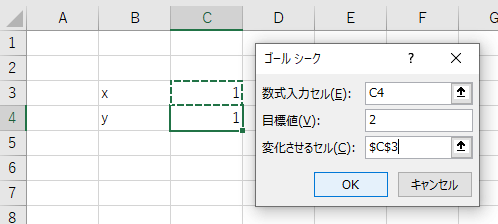
ゴールシークを起動して、下のように条件を入力してOKを押します。

「数式入力セル」　：C4を選択
「目標値」　　　　：「2」
「変化させるセル」：C3を選択

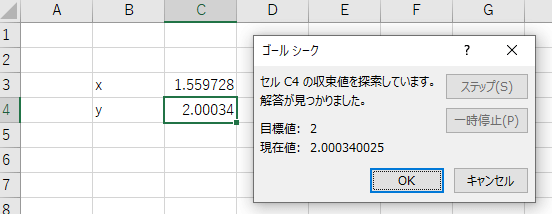
この設定で計算をスタートすると無事に解答が見つかって、答え$x$を返してくれました。
解答（$x$）は1.559728で、
その時の計算結果の値（$y$）は2.00034となりました。

解答が見つからない場合もある

ちなみに、初めに入れておく$x$の値を1ではなく100にしてゴールシークを始めたときは、時間内に答えを見つけることができません。

試してみると、下の画像のような結果が表示されました。

100から計算を試して、87.2393・・・で力尽きています。

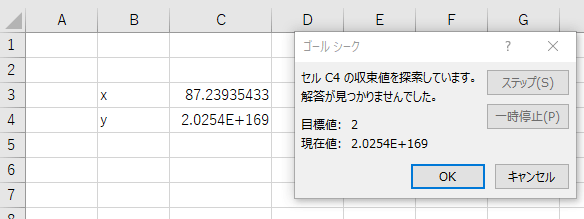
このように、初めに入れておく$x$の値によっては計算が終わらないこともあるので、ざっくりとでも答え（$x$）がわかっている時は、答えに近い$x$の値にしておく方が無難です。

『$100^{100}$は桁が大きすぎるな・・・。$2^2=4$、$1^1=1$だから、$x$は1～2の間の数かな？』と、ざっくりとでもわかっていれば、初めの$x$の値を1か2にしておけばOKです。

対数を取ると計算が早く完了することもある？

初めに入れておく$x$の値を100とすると、上で見たように計算が完了しませんでしたが、あらかじめ今回の式を少し変形しておくと計算がちゃんと完了しました。

（コンピューター科学に疎いのでよくわかりませんが、）計算処理に負担のかかる（時間のかかる）式とそうでない式というのがあるのかなと思います。

具体的には、元の式の両辺で、常用対数を取って「$x^x=2$」を「$x\log_{10}{x}=\log_{10}{2}$」としておきます。（別に常用でなくても普通の指数$\log_{e}$でも良いです）


C3（初めの$x$の値）は100
C4の計算式は「=C3*log10(C3)」　と入力。
後でゴールシークの入力をする時の確認用に、C6のセルに「=log10(2)」の値を計算しておきます。

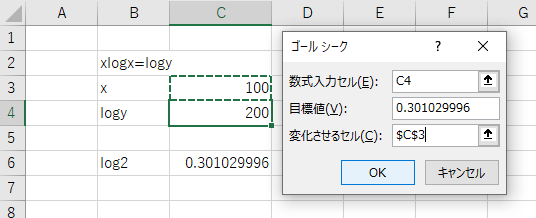
あとはこれまでの例と同じように、メニューの「データ」→「What-If分析」→「ゴールシーク」を選択し、条件を入力してOKで計算を開始します。
※「目標値」を手打ち入力する際に先ほどのC6の結果を見ながら入力します。


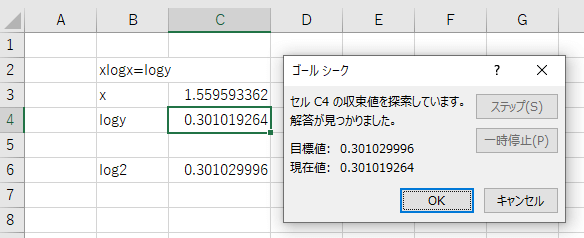
初期の$x$の値は計算不可だった時と同じ100から始めてますが、今回はちゃんと計算が完了して$x$の値を知ることができました。

$x=1.559593362$です。（$x^x=2$の$x$初期値1で実施した結果と微妙に異なりますが・・・細かいことは今回は気にしないことにします）

ゴールシークの欠点・デメリット

ゴールシークは上で見てきたようにとても便利なツールですが、いくつか欠点・デメリットがあります。

実数しかわからない

計算結果は実数で返ってきます。そのため、数学の方程式を解いて求めるように分数や複素数の解までは知ることができません。

あくまでも計算結果として、実数をサクッと計算してほしい時、に使うようにしましょう。

近似値（小数）しかわからない

また、分数も表現できないため、答えはいつも、ずら～～～っと続く小数でしか知ることができません。

表示されているのはあくまで「近似値」「近い数」であることを理解してゴールシークを使う必要があります。

ひとつしかわからない

ゴールシークを使うと、計算結果として$x$の値をひとつだけ知ることができます。

例えば2次方程式の解のように、いくつかの実数解を持っていたとしても知ることができるのはひとつだけです。

そのため、ひとつだけ答えがわかればいい時、にしか使えません。全く得体の知れない式でゴールシークを使う時は、実は他にも答えがあるかもしれないので要注意です。


このようにいくつか欠点のあるゴールシークですが、使い方次第で複雑な計算もサクッと終えることができるので、上手く活用したいですね。

今まで、式変形や方程式に使っていた時間を省略することができるかもしれません。

まとめ：ゴールシークは複雑な計算で威力を発揮するツール

簡単な方程式の計算であれば普通に解いた方が早くて正確ですが、今回のように（$x^x=2$）ちょっと簡単には答えを求められない複雑な式の時に、紹介したゴールシークが威力を発揮します。

いくつかの欠点もありますが、『ちょっとこの計算面倒～！』という時にとっても役立つと思うので、ぜひ活用してみてください＾＾

指数の計算にも使えるので、例えば『元金と利率から、〇年後にいくら（目標額）になるか？』みたいな計算にも使うことができますよ。

・元金：100万円
・年利：3%
・目標：200万円

なら、『$100\times1.03^x = 200$』をゴールシークで計算して出てくる$x$が、知りたい「何年後」の答えですね。